Dernière mise à jour le 22 avril 2021 par LMD

Le diagramme de Voronoï est un pavage du plan constitué de polygones juxtaposés, à l’intérieur desquels se trouve l’un des points d’origine.
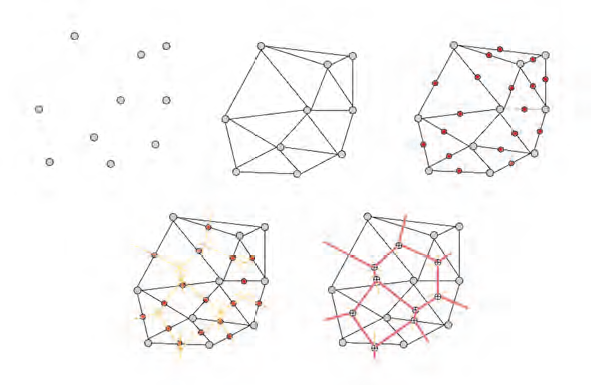
Le diagramme de Voronoï est construit à partir d’une série de points. Chaque point est relié aux deux points les plus proches pour constituer des triangles juxtaposés par leurs sommets et/ou leurs côtés. Les liaisons sont matérialisées par des segments dont on construit ensuite les médiatrices. Les intersections des médiatrices sont marquées par des points (indiqués par une croix) qui seront reliés entre eux par des segments (en rouge sur la figure ci-dessous) pour constituer le diagramme de Voronoï.

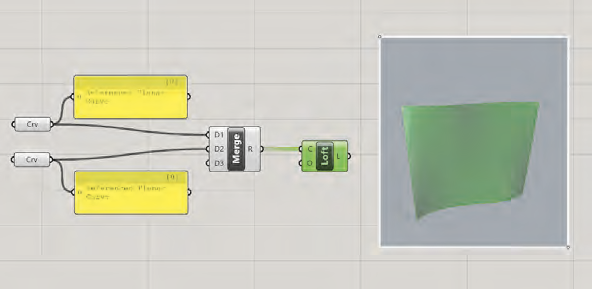
Création d’une surface gauche à partir de deux courbes génératrices

découper une surface gauche verticale épaissie en structure ajourée (selon le motif fourni par les cellules de Voronoï)

Nous commençons cette démonstration par la création d’une surface gauche verticale qui sera considérée comme une portion de paroi verticale à traiter. La surface est générée à partir de deux courbes dessinées sur le plan XY (pour une démonstration complète du présent exercice, les courbes doivent être dessinées à proximité de l’intersection des axes X, Y et Z, dans le premier cadran (X > 0 et Y > 0) et dans une direction voisine de l’axe X). L’une d’elles sera déplacée dans la direction de l’axe Z au-dessus du plan XY, l’autre reste dans le plan XY.
L’intégration des deux courbes dans Grasshopper s’effectue via le composant Params>Geometry> Curve . Ce composant sera utilisé à deux reprises pour associer les deux courbes en suivant le même processus que celui utilisé pour la réalisation de la tour paramétrique.

Nous utilisons le composant Sets>Tree>Merge pour rassembler les deux courbes et les connecter ensuite au composant Surface>Freeform>Loft pour générer la surface à traiter.

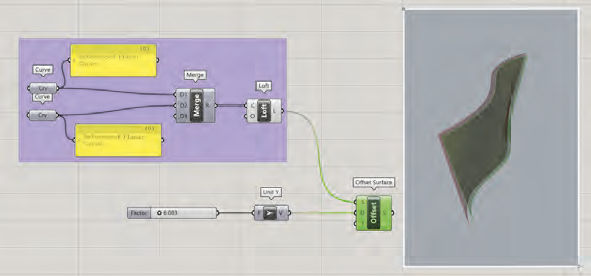
Génération d’un volume fermé à partir de surfaces gauches

Afin de donner une épaisseur à la surface d’origine, nous utiliserons le composant Surface>Util>Offset Surface. Ce dernier a besoin d’un vecteur pour définir la direction et l’amplitude du décalage de la surface d’origine. Pour notre cas, nous avons besoin d’un composant
Vector>Vector>Unit Y connecté à un Number Slider pour fixer ce paramètre (entrée D). La surface d’origine (résultat du composant Loft) sera reliée à l’entrée S du composant Offset Surface.

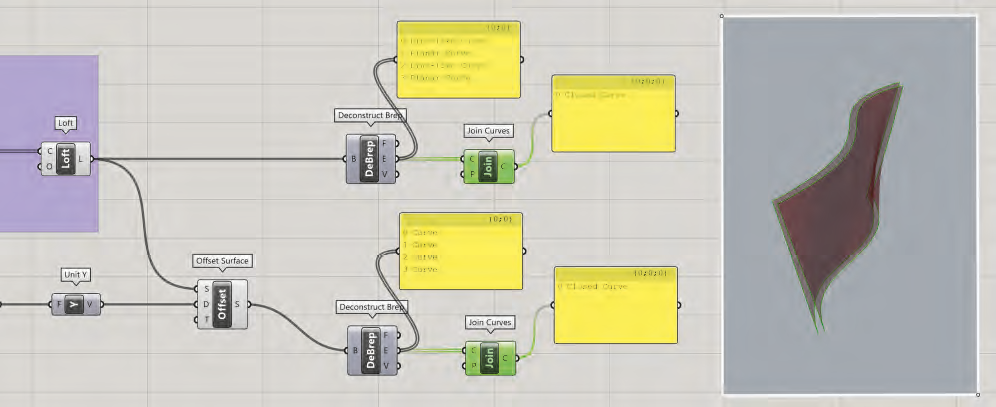
Décaler une surface
Pour épaissir une surface, le composant Offset Surface fonctionne bien quand le vecteur placé à son entrée D reste majoritairement orthogonal au plan de la surface que l’on duplique. Son fonctionnement
est inefficace sur une surface gauche qui présente des parties presque en alignement avec le vecteur placé sur l’entrée D : à cet endroit, l’épaississement devient nul, voire négatif car la surface décalée va se replier sur elle-même.
Nous obtenons ainsi deux surfaces « voisines », en regard l’une de l’autre, distantes de la valeur fixée par le Number Slider correspondant.
La création de la surface s’appuyant sur les bords des deux surfaces précédentes, en forme de ruban, nous offrira la possibilité de générer un volume fermé (Closed Brep), indispensable pour la suite des opérations. Pour créer ce ruban, il faut isoler les contours de chacune des surfaces
gauches. Cette tâche sera possible grâce à la combinaison de l’outil Surface>Analysis>Deconstruct Brep pour isoler les contours et de l’outil Curve>Util>Join Curves afin de les relier et de créer un seul contour fermé pour chacune des surfaces. Cette combinaison sera appliquée à
la surface gauche d’origine ainsi qu’à la surface décalée.

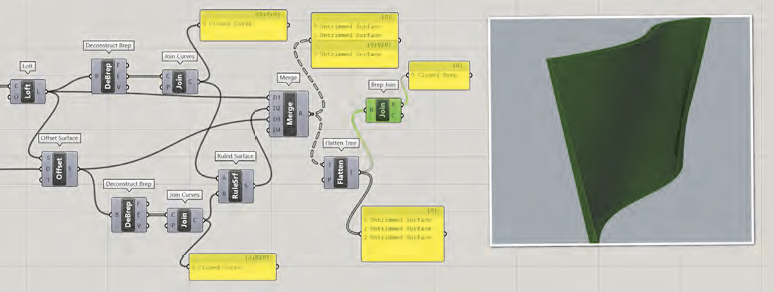
La création du ruban sera réalisée par le composant Surface>Freeform>Ruled Surface en reliant les sorties des deux composants Join Curves. Nous rassemblons les trois surfaces via le composant Sets>Tree>Merge. La sortie de ce composant sera connectée au composant Surface> Util>Brep Join pour générer un volume fermé (Closed Brep).
Cependant, cette opération n’est pas immédiate car, telle quelle, la sortie du composant Merge se présente sous la forme d’un arbre contenant deux branches : la première, identifiée {i}, contient la surface d’origine et son offset, et la seconde, identifiée {0 ;0 ;i}, contient le ruban.
On va donc intercaler un composant Sets>Tree>Flatten Tree pour transformer l’arbre en liste.
Ainsi, le composant Brep Join fournit bien, à sa sortie, un volume fermé closed brep.

Création de cellules Voronoï 3D

Nous commençons cette étape par la création d’une « boîte englobante », qui est mathématiquement un parallélépipède. Son type de donnée est box et elle présente la particularité d’entourer au plus juste l’objet géométrique placé à son entrée. Nous allons y créer des cellules
de Voronoï en 3D.
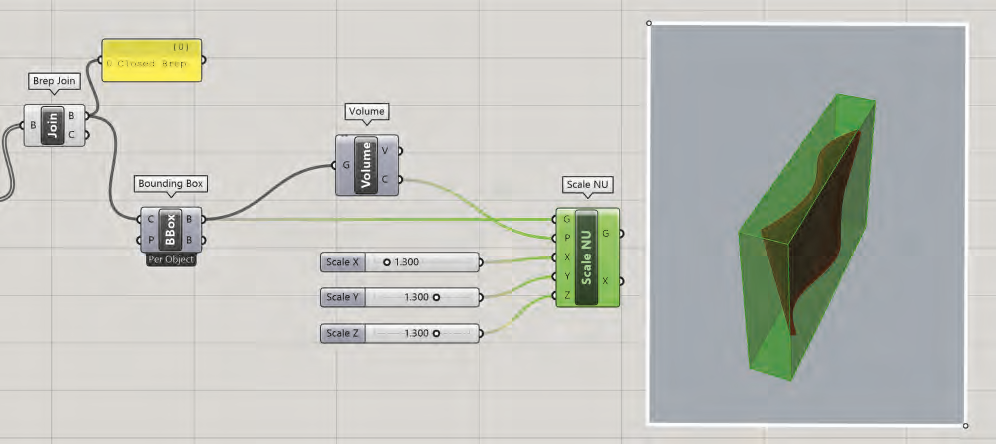
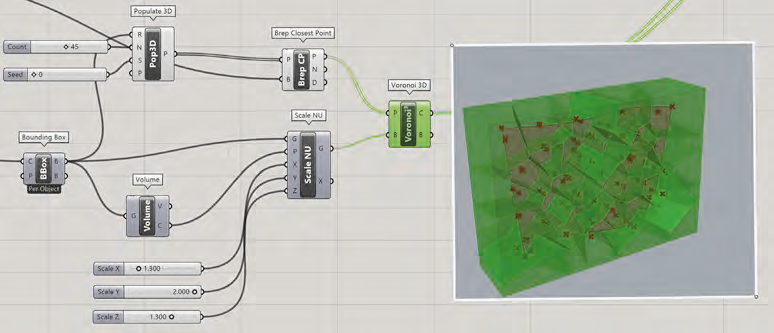
Le composant Surface>Primitive>Bouding Box offre la possibilité de générer la boîte englobante de la géométrie placée sur son entrée C. Ce parallélépipède sera redimensionné avec un facteur d’échelle de 1.3 sur les trois axes en exploitant le composant Transform>Affine>Scale NU.
Le centre de la mise à l’échelle est défini par le composant Surface>Analysis>Volume connecté à la sortie B du composant Bounding Box.
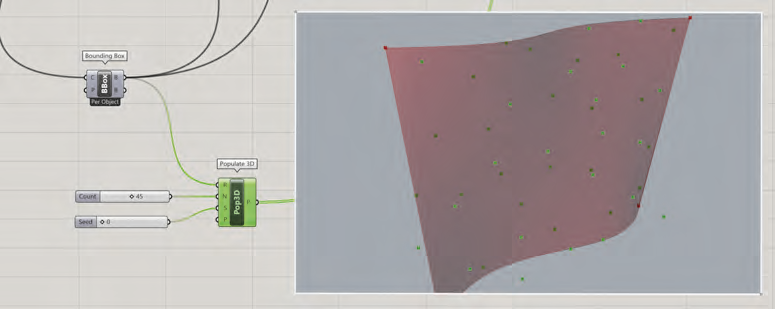
Les cellules de Voronoï en 3D sont créées à partir de points placés de manière aléatoire sur l’une des surfaces gauches. Le composant Vector>Grid>Populate 3D a besoin d’une boîte fermée pour générer une population de points. Son entrée R sera connectée à la sortie B
(pour box) du composant Bounding Box.

Le composant Populate 3D a besoin de deux paramètres :
• un premier Number Slider de type entier variant entre 1 et 100 pour l’entrée N, définissant ainsi le nombre de points à créer ;
• un second Number Slider de type entier variant entre 1 et 1 000 pour définir le mode de traitement aléatoire de la répartition des points.

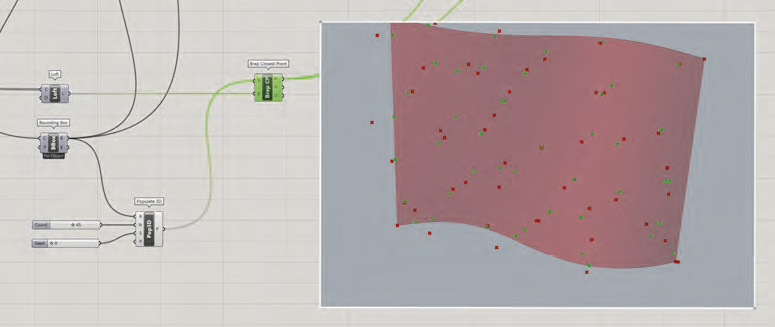
Les points générés par ce composant sont ensuite triés pour sélectionner uniquement les points en contact avec cette surface (ce qui n’est pas le cas de l’ensemble des points générés par le composant Populate 3D). La sélection de ces points sera assurée par le composant Surface>Analysis>Brep Closes Point dont l’entrée P sera reliée à la sortie P du composant Populate 3D et l’entrée B sera connectée la sortie L du composant Loft.

Les points générés sont connectés au composant Mesh>Triangulation>Voronoï 3D, créant ainsi les cellules de Voronoï en 3D délimitées par le volume englobant défini par le composant
Bounding Box et mis à l’échelle par Scale NU.

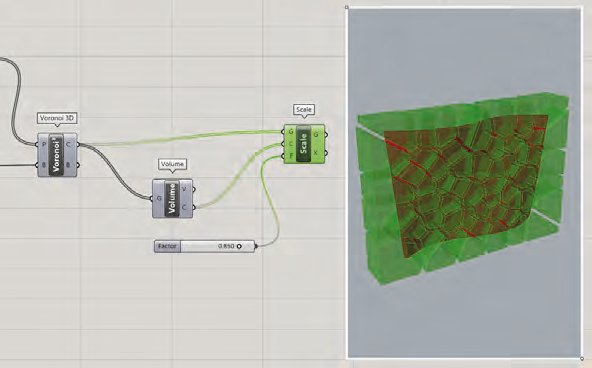
Nous utilisons le composant Transform>Affine>Scale pour réduire la taille des cellules de Voronoï en 3D et créer un décalage entre elles que nous allons exploiter par la suite. La mise à l’échelle se fera en utilisant les barycentres des cellules 3D identifiés à l’aide du composant
Surface>Analysis>Volume. Un Number Slider de type réel, variant entre 0 et 1, sera utilisé pour définir le facteur d’échelle (nous testons avec la valeur 0.85)

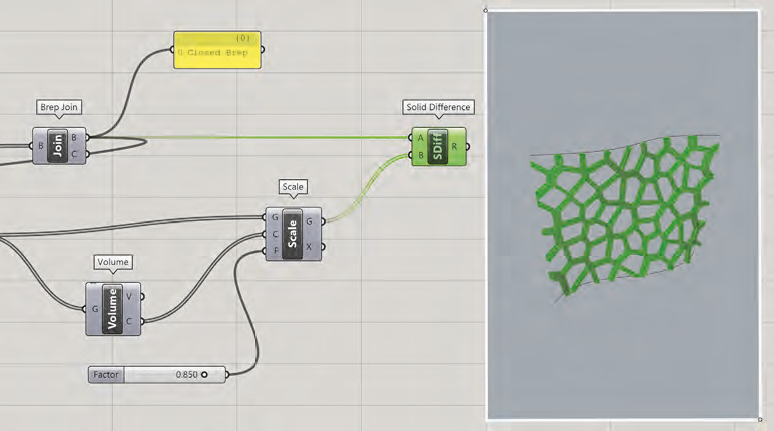
Le composant Intersect>Shape>Solid Difference permet de créer une opération booléenne de soustraction de matière entre le premier volume (surface gauche avec épaisseur) et les différentes cellules mises à l’échelle. Ce composant ne fonctionne qu’avec des volumes fermés (closed breps) sur ses deux entrées A (solide à découper) et B (solide découpant). Dans sa modélisation paramétrique, le concepteur doit donc penser à aboutir forcément sur des volumes fermés dans sa
chaîne paramétrique dès qu’il sait qu’il aura à utiliser au final le composant Solid Difference.

Utilisation du composant Scale NU
Ce composant permet de mettre à l’échelle un objet dans les trois directions (X,Y et Z). La valeur d’échelle dans chacune des directions est définie par un composant Number Slider. Cette opération de transformation nous permet de créer des cellules de Voronoï en 3D dont les limites dépassent celles de la surface gauche initiale épaissie. Cette fonction permet de garantir une intersection parfaite entre les cellules
de Voronoï en 3D et le volume gauche (pas de chevauchement de surfaces ou de volumes qui peuvent générer des bavures au moment de l’intersection).